Die Leipziger Volkszeitung: Name <----- 0.42 -----> Kürzel
Dies ist der erste Artikel aus einer losen Sammlung von Texten über die Leipziger Volkszeitung und ihre ca. 365.000 Artikel aus den Jahren 2010 bis 2021, die ich auswerte (Work in Progress und so). Hier geht es darum, das Geflecht aus Autor:innen und ihren Kürzeln zu entwirren.
Warum das Ganze?
Die Motivation, journalistische Beiträge in einer Data Science Manner zu untersuchen, habe ich Zeit Online (ZON) und David Krisel zu verdanken. ZON hat 2019 für ihre Auswertung der Protokolle des Deutschen Bundestages den Grimme Online Award gewonnen. ZONs Auswertung hat dabei vor allem meine Analyse der Artikel der Leipziger Hochschulzeitung motiviert. Die nächste logische Stufe nach der Hochschulzeitung ist Leipzigs einzige Tageszeitung: die LVZ. In meinen kommenden Auswertungen knüpfe ich nah an den mittlerweile recht berühmten Talk vom Datenanalysten David Kriesel auf dem 33. Chaos Communication Congress an. In „SpiegelMining“ geht es - wie man sich denken kann - um die Auswertung von Spiegel Online Artikeln. Ich will gar nicht viel spoilern, aber wie Kriesel nur anhand von Metadaten potentielle Liebschaften in der Redaktion aufdeckte, gibt einem einerseits ein bisschen zu denken und ist gleichzeitig wirklich sehr beeindruckend.
Nach dem Anfang ist vor dem Anfang
Dies ist der erste Artikel in dieser Serie, aber eigentlich müsste ihm ein anderer vorausgehen. Der würde beschreiben, wie ich die LVZ gescraped habe, wie die Artikel aufgebaut sind, was so alles auf lvz.de veröffentlicht wird ecetera ecetera. Dieser Artikel erscheint nun zuerst, weil er in diese „got over-excited about the tech, and jumped into coding too early“-Kategorie fällt.
All ML projects which turned into a disaster in my career have a single common point:
— Francesco Pochetti (@Fra_Pochetti) March 12, 2022
🚨 I didn't understand the business context first, got over-excited about the tech, and jumped into coding too early.
Insbesondere standen für mich in meinen Kopf die Auswertungen der Metadaten vor den semantischen Analysen der Texte. Das heißt, erst einmal herausfinden, wer in der Redaktion was mit wem hat und danach Word Embeddings berechnen. Doch gerade als ich loslegen wollte, stach mir eine Zahl ins Auge, die mich störte. Etwa 21 Prozent der Artikel der LVZ werden unter einem Kürzel veröffentlicht. So zum Beispiel der eingeblendete Artikel unter diesem Absatz. Er wurde von Robert Nößler und einer weiteren Person veröffentlicht, die hier nur mit ihrem Kürzel „tsa“ unterschrieben hat. Diese Kürzel als eigene Autorenentitäten zu behandeln, würde zu kurz kommen und eventuell spätere Auswertungen verzerren. Denn eigentlich ist es dieselbe Autorin, ob sie nun unter Klarnamen oder Kürzel veröffentlicht. Und die Statistik, die besagt, dass die Redaktionsmitglieder Liebschaften mit ihren eigenen Kürzeln unterhalten, weil sie sich zufällig wirklich immer zu selben Zeit Urlaub genehmigen, würde meine Freude trüben.
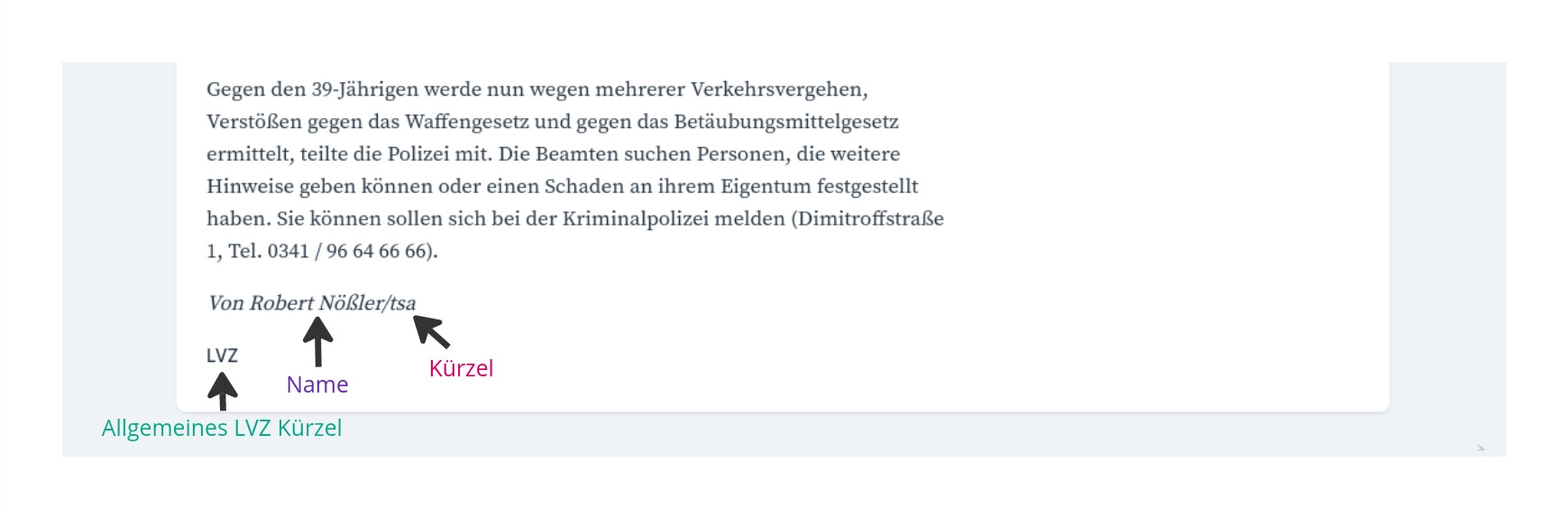
Das typische Ende eines LVZ Artikels. Unterschrieben mit einem Kürzel und einem Klarnamen.
Ergo brauchen wir ein Mapping zwischen Kürzel und Klarnamen. Geübte Zeit- oder Spiegel-Online (oder irgendein anderes Onlineportal) Leser:innen werden sich nun vielleicht fragen: Ist es nicht möglich, auf ein Kürzel oder einen Namen zu klicken und zu einer Art Autorenseite zu gelangen? Die Antwort: Jein. Dieses Feature hat nämlich erst mit der Neugestaltung der LVZ-Website im Jahr 2023 Einzug gefunden. Und auch nur zu Teilen. Artikel, die mit einem Kürzel unterschrieben sind, bieten dieses Feature weiterhin nicht. Für alle anderen Artikel gilt: Es ist kompliziert. Sehr kompliziert.
Wie ich die Autor:innenkürzel und -namen für die 365.000 Artikel extrahierte, darüber wird der nächste Artikel berichten. Kleiner Teaser: Das ganze Prozedere stützt sich dabei weitestgehend auf heuristikbasiertes Regex Matching, Natural Language Processing und Active Learning.
Ein Moving Window
Wie nun starten mit dem Mapping? Zunächst müssen wir ein paar Grundannahmen treffen. Diese leiten sich davon ab, wie ich darüber denke, wie die Kürzel vergeben werden und von tatsächlichem Wissen über diese Zuweisungen, das mir von LVZ-Autor:innen gesteckt wurde. Daraus formulierte ich folgende drei Hypothesen:
- Es gibt keine irgendwo innerhalb der LVZ dokumentierten konkreten Regeln (Wissen)
- Alle Kürzelbuchstaben sind auch im Namen enthalten (Annahme)
- Die Kürzelbuchstaben tauchen in derselben Reihenfolge im Kürzel sowie im Namen auf auf (Annahme)
Aus diesen Hypothesen schusterte ich eine Suche zusammen. Für jedes Kürzel wird in der Menge der Autor:innennamen ein passendes Gegenstück gesucht. Dabei erschien es mir sinnvoll, die Menge der Namen zeitlich um das Auftreten des Kürzels herum, einzugrenzen. Ein Autor mit einer Handvoll Artikeln in 2010 und 2011 wird wohl keinem Kürzel zugeordnet sein, das seinen ersten Auftritt unter einem Artikel in 2020 hatte. Das Ganze kann man sich wie ein Moving Window vorstellen, was mit einem Parameter X in den letzten X und kommenden X Monaten nach Namen sucht.
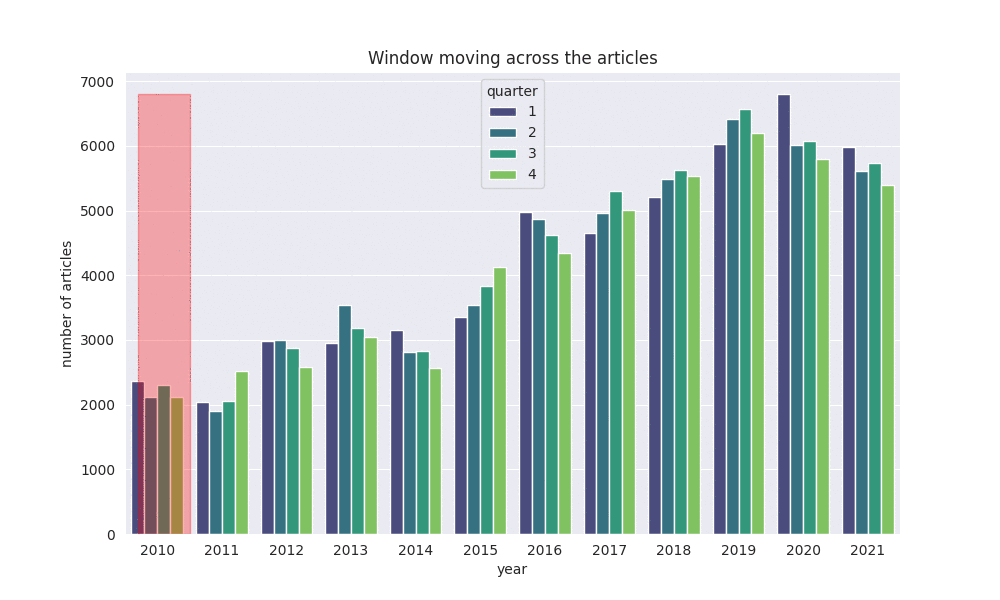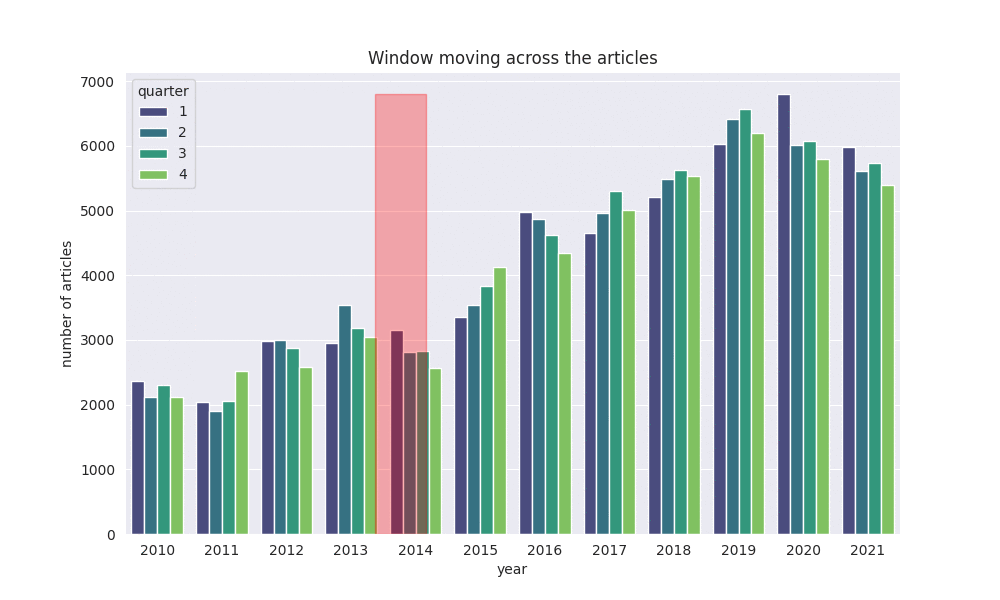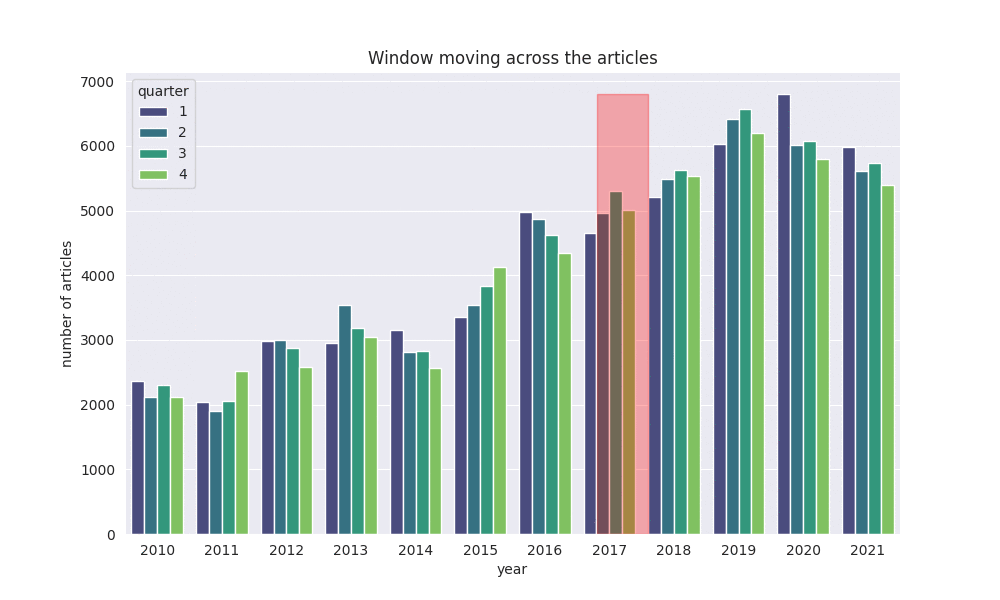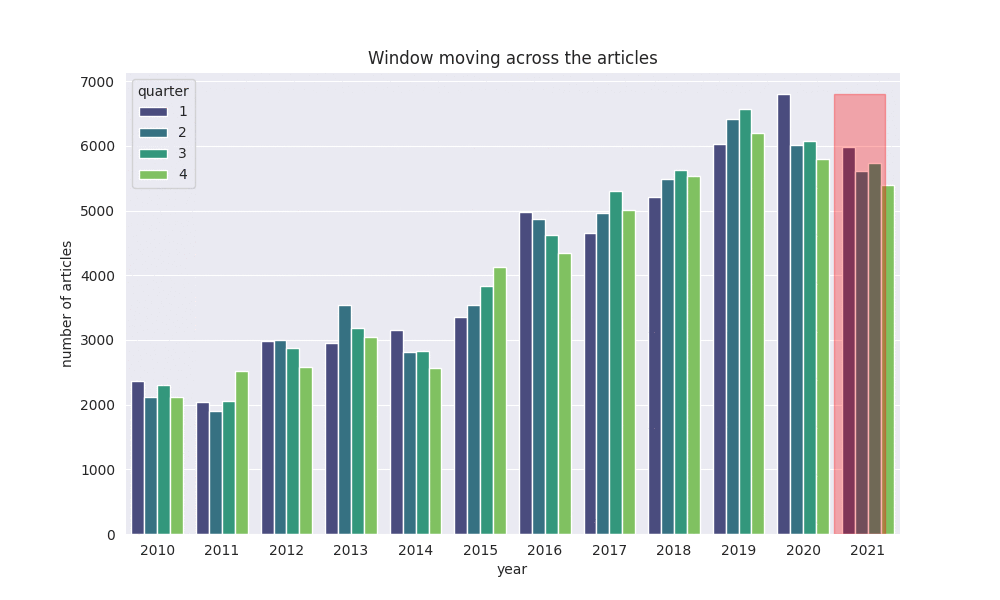
Das Moving Window sucht hier 6 Monate in der Vergangenheit und Zukunft nach passenden Namen.
Eine einfache Heuristik berechnet dabei einen ersten Score auf Basis von semantischen Ähnlichkeiten zwischen Namen und Kürzeln. Ein fiktives Beispiel: der Name Gudrun Hagen bekommt für das Kürzel „GH“ einen höheren Score zugewiesen als Wolfgang Lehmann, obwohl dieser auch beide Buchstaben enthält.
Lassen wir uns ein Blick auf diese erste Analyse werfen. Wie in der folgenden Grafik zu sehen, plotte ich die Anzahl der geschriebenen Artikel pro Quartal des Kürzels (engl.: Abbreviation) und von den potentiellen dazugehörigen Klarnamen. Das kann das wie links oben sehr vernünftig aussehen, wo dem Kürzel der in Orange statt in Grün dargestellte Name zugeordnet wurde. Wie rechts oben dargestellt, kann es aber auch mehr Fragen aufwerfen und man kann sich wundern, wie konsequent und logisch nachvollziehbar LVZ-Redakteur:innen ihr Kürzel eigentlich einsetzen. Links unten werden wir ganz alleine gelassen und rechts unten können wir sagen, dass mit zu wenig Datenpunkten einfach kein Matching möglich ist.
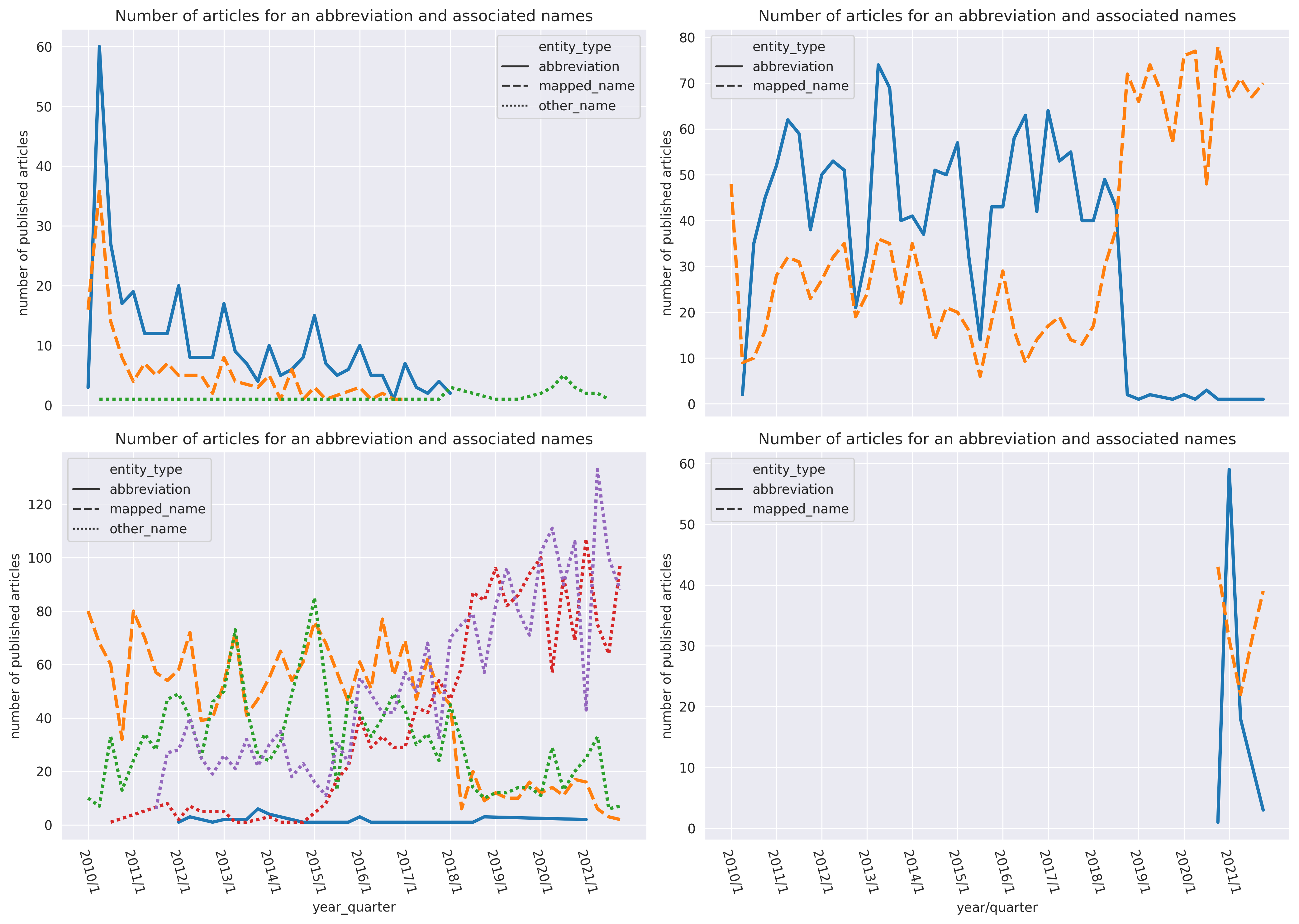
Die Anzahl an geschrieben Artikel pro Quartal von vier Kürzel und ihre semantisch dazugehörigen Namen.
Beim Durchschauen der Grafiken kann man dem semantischen Matching aber schon Credits geben. Viele Matchings sehen valide aus. Das Schwierige an dieser Auswertung wird mich auch in den folgenden Schritten noch begleiten: Ich habe kein Validierungsset. Ich kann nicht testen, ob Kürzel XY nun tatsächlich zum Autor XY gehört.
Das heißt, ich musste anders evaluieren, wie das Matching abschneidet. Als Informatiker macht man das natürlich auch gerne mit der ein oder anderen Zahl. Deshalb errechnete ich den Pearson-Korrelationskoeffizient, um zu testen, ob die Anzahl der geschrieben Artikel pro Quartal von Kürzeln und Namen positiv korrelieren. Die Summe über die Koeffizienten aller Mappings ergab dabei eine positive Korrelation. Von 0,07. Das ist wirklich noch ausbaufähig. In der folgenden Grafik sehen wir die Entwicklung des Koeffizienten, basierend auf der Anzahl an Datenpunkten auf dem er berechnet wurde. Werfen wir einen Blick zurück auf die vier Grafiken oben, können wir besonders an der unten rechts schon erahnen, dass das Korrelationsmaß bei wenig Datenpunkten auch wenig aussagekräftig sein wird. Schauen wir uns jetzt die Entwicklung an, können wir immerhin (trotz des Ausreißers bei 40 Datenpunkten) eine zunehmende Sicherheit bei mehr Daten feststellen.
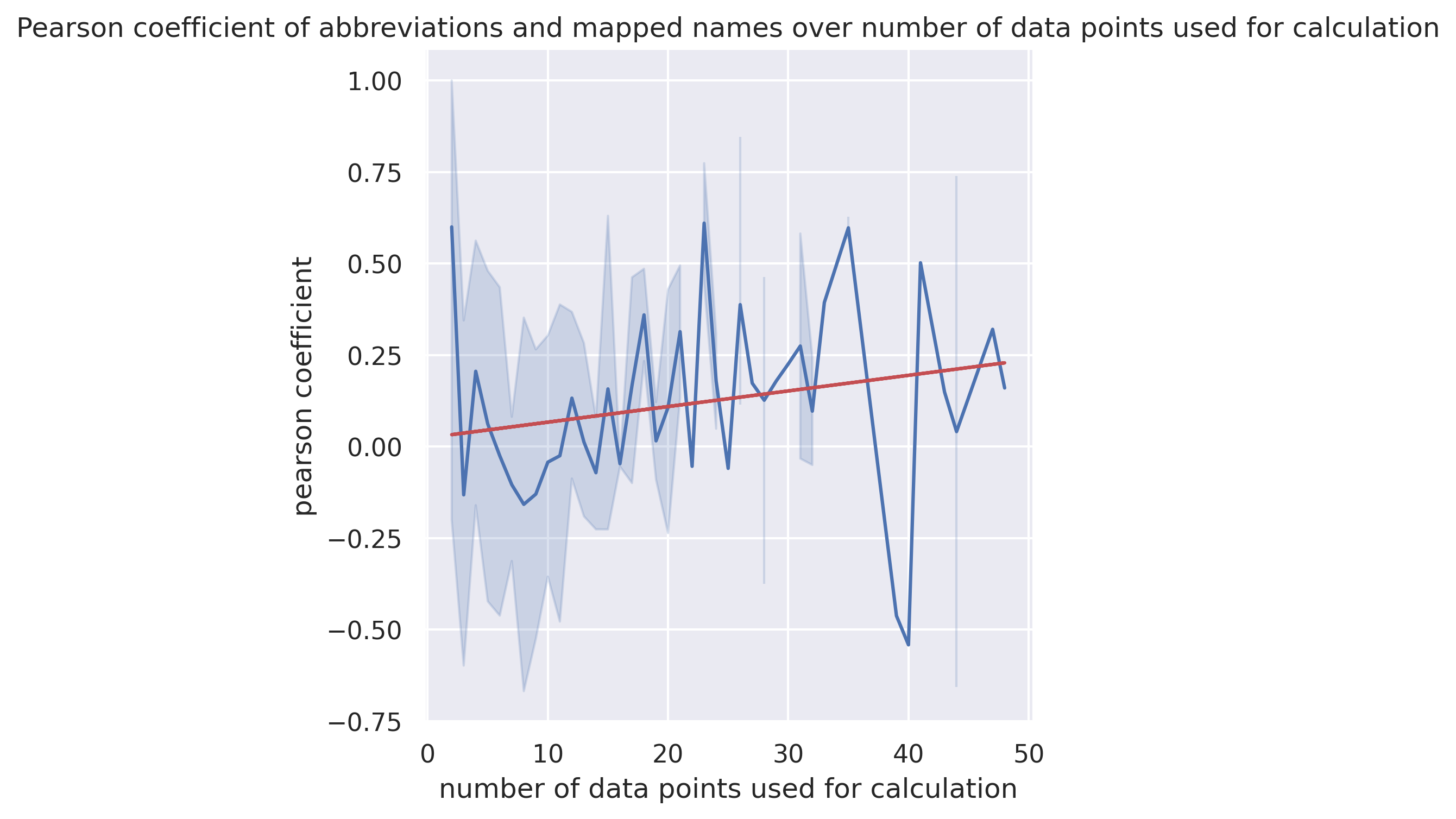
Der Pearson-Korrelationskoeffizient für die Verteilung der geschrieben Artikel zwischen Kürzel und Namen über die Anzahl an verfügbaren Datenpunkten.
Übrigens: Für den Autor in den Grafiken oben rechts, wo ich dank etwas Recherchearbeit weiß, dass das Mapping stimmt, ergibt die Berechnung eine negative Korrelation von -0,65. Wenn wir nur die Werte bis Mitte 2018 betrachten, sind es immerhin 0,45. Das heißt, die Korrelation ist keine perfekte Metrik, um das Zusammengehören festzustellen.
Trotzdem ist das Korrelationsmaß eine Basis für die Bewertung der Verbesserungen, die ich am Mapping vornehmen werde. Und was das für Verbesserungen sind, erfahrt ihr jetzt.
Frequenzanalyse
Nach der semantischen Analyse habe ich nun einen Score für jede passende Verbindung zwischen Klarnamen und Kürzel für jeden Artikel, der mit einem Kürzel unterschrieben ist. Das kann man sich ungefähr so vorstellen:
| Article ID | Abbreviation | Name | Semantic Score |
|---|---|---|---|
| 1 | GH | Gudrun Hagen | 0.8 |
| 2 | GH | Wolfgang Lehmann | 0.333 |
| 3 | Wol | Wolfgang Lehmann | 0.7 |
| 4 | WL | Wolfgang Lehmann | 0.8 |
Nun kann es passieren, dass es einen Namen gibt, der wie die Faust aufs Auge für das Kürzel passt. Zum Beispiel würde in unserem Beispiel das Kürzel „WL“ sehr gut zu Herrn Wolfgang Lehmann passen. Aber diesen passende Fit gibt es vielleicht nur für einen Artikel (ID: 4), weil das Kürzel „WL“ Ende der 2010er geschrieben hat und Wolfgang Lehmann Anfang der 2010er aber er hat gegen Ende des Jahrzehnts dann noch einen letzten Artikel (ID: 4) veröffentlicht. Davon ausgehend, würde es mehr Sinn ergeben, ihm „Wol“ zuzuordnen und „WL“ bekommt dann wer anderes.
Um solche Fälle zu erfassen, errechne ich zwei Prozentanteile:
- Der Anteil des Namens Wolfgang Lehmann von allen Namen auf die as Kürzel „WL“ zeigt (Abbreviation pointing to Name Share)
- Der Anteil des Kürzels „WL“ von allen Kürzeln auf die der Name Wolfgang Lehmann zeigt (Name pointing to Abbreviation Share)
Erweitern wir unsere Tabelle um diese beiden Prozentanteile. Ein kleines Rechenbeispiel: Das Kürzel „GH“ zeigt auf zwei Namen, je einmal pro Namen. In 50 Prozent der Fälle zeigt es auf Gudrun Hagen und in den anderen 50 Prozent auf Wolfgang Lehmann. Der Name Wolfgang Lehmann zeigt einmal auf „GH“, einmal auf „Wol“ und einmal auf „WL“. Die drei Kürzel bekommen deshalb einen Anteil von je einem Drittel.
| Article ID | Abbreviation | Name | Semantic Score | Abbreviation pointing to Name Share | Name pointing to Abbreviation Share |
|---|---|---|---|---|---|
| 1 | GH | Gudrun Hagen | 0.8 | 1/2 | 1/2 |
| 2 | GH | Wolfgang Lehmann | 0.333 | 1/2 | 1/3 |
| 3 | Wol | Wolfgang Lehmann | 0.7 | 1 | 1/3 |
| 4 | WL | Wolfgang Lehmann | 0.8 | 1 | 1/3 |
Anhand dieser Prozentanteile berechne ich einen Frequenz-Score, der mit auf das endgültige Matching einzahlt.
Ressortangehörigkeiten
Die LVZ unterhält mehrere regionale Büros. Zum Beispiel in Altenburg oder in Grimma. Dabei werden diese Lokalausgaben teilweise unter eigenen Namen veröffentlicht. So zum Beispiel berichtet die Osterländer Volkszeitung (OVZ) über den Landkreis Altenburger Land. Da die LVZ als Lokalzeitung einen starken Regionalbezug hat, sind auch die entsprechenden Ressorts unter den Meistpublizierenden. Dabei haben diese Ressorts ihre zugewiesenen Autor:innen. Es kann einem also komisch vorkommen, wenn ein Kürzel fast ausschließlich in Altenburg veröffentlicht, aber mein semantischer Algorithmus ihm einen Namen aus dem Büro Delitzsch-Eilenburg zuweisen möchte. Immerhin wären das 80 Kilometer ständiges Pendeln. Deshalb errechne ich noch einen weiteren Score: Wie ähnlich sind sich die Ressortangehörigkeiten von Name und Kürzel.
Earth Mover's Distance
Um zu erfassen, wie ähnlich diese Angehörigkeiten sind, greife ich auf die Earth Mover's Distance zurück. Die numerischen, formalen Definitionen überlasse ich euch zum Selbststudium. Zusammengefasst kann man die Distanz so beschreiben: Die Earth Mover's Distance (EMD), auch als Wasserstein-Distanz bekannt, ist ein Maß für die Unterschiede zwischen zwei Wahrscheinlichkeitsverteilungen. Sie misst die minimale durchschnittliche Arbeit, die erforderlich ist, um eine Verteilung in eine andere zu transformieren.
Um die EMD zu verstehen, kann man sich vorstellen, dass die beiden Wahrscheinlichkeitsverteilungen als Mengen von Erdmengen betrachtet werden. Jede Menge repräsentiert eine Verteilung von Ressourcen oder Masse. Die EMD misst dann die minimale Arbeit, die benötigt wird, um die Masse von einer Verteilung in die andere zu transportieren. Dabei wird der Abstand zwischen den Massen gewichtet und berücksichtigt.
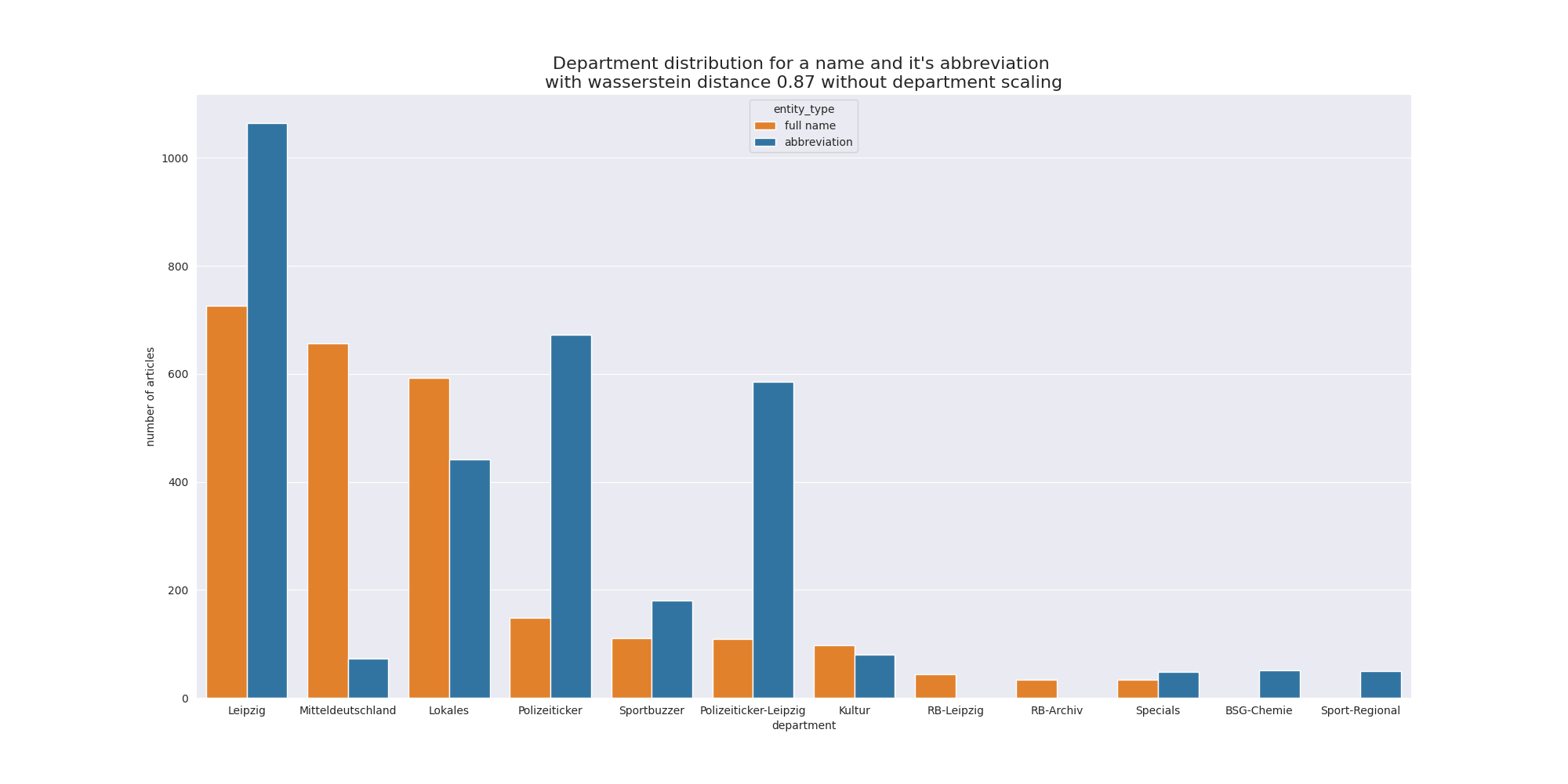
Wie viel Arbeit brauchen wir, um die orangene Verteilung in die Blaue umzuwandeln?
Oben sehen wir eine Earth Mover's Distance von 0,87 (0 ist das Beste) bei einem Namen und Kürzel, die - wieder dank kleiner Recherche - zusammengehören.
Ressorts skalieren
Autor:innen entscheiden sich nicht zufällig, ob sie unter den Artikel ihr Kürzel oder ihren vollen Namen setzen. Kürzere Artikel wie zum Beispiel Meldungen werden eher mit einem Kürzel unterzeichnet als eine ganze Reportage über viele tausende Zeichen. Auch Gemische wie das Anreichern von Agenturmeldungen wie zum Beispiel von der DPA oder Reuters werden gerne mit Kürzeln unterschrieben.
Um diesem Effekt vorzubeugen, habe ich mir die Ressorts näher angeschaut. Tatsächlich gibt es einige Ressorts, die viel mehr das Kürzel als Unterschrift nutzen als den ganzen Namen und ebenso auch andersherum. Wenn man sich die Namen der Ressorts anschaut, ergibt das auch durchaus Sinn.
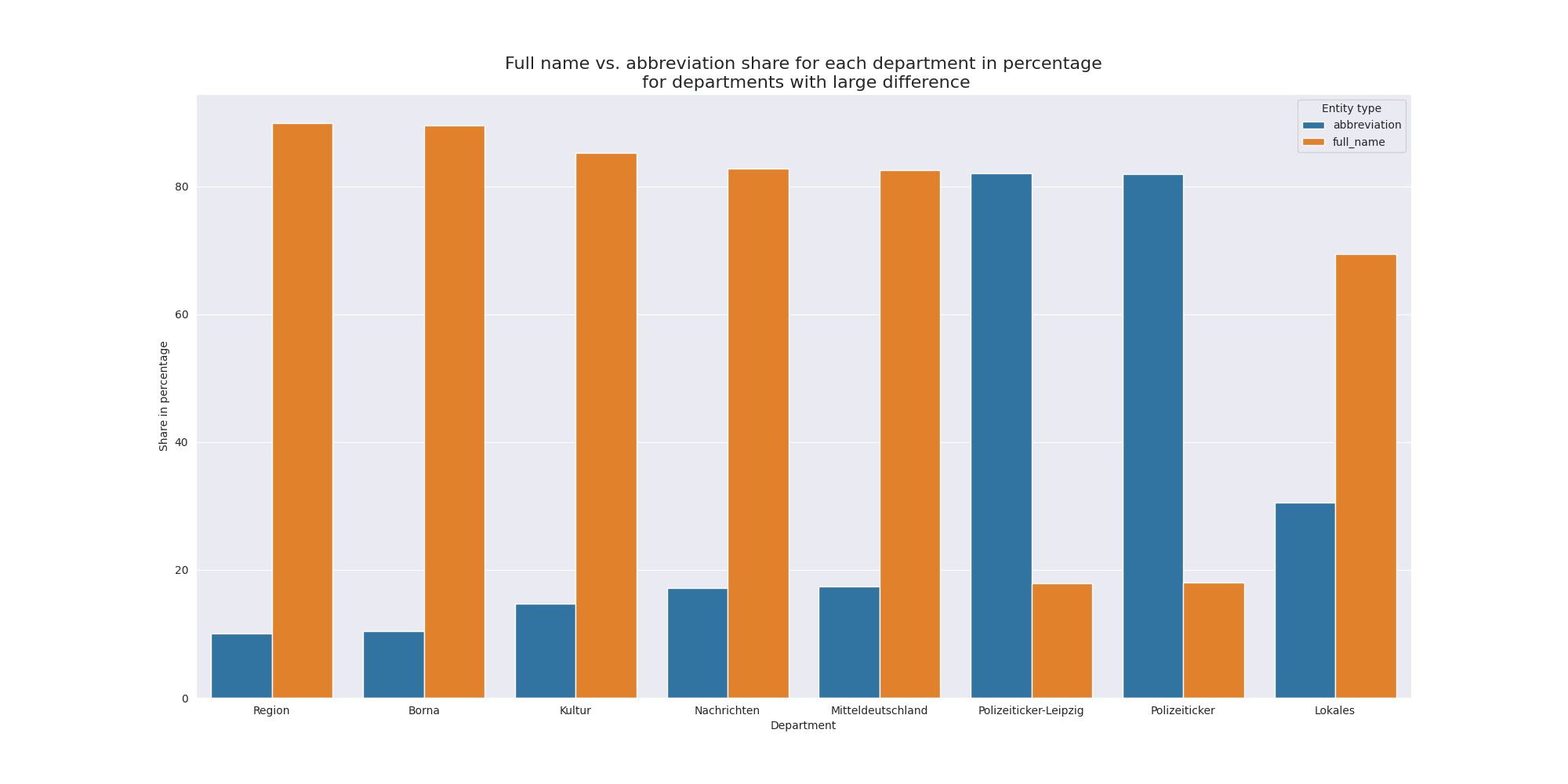
Die Ressorts mit der größten Lücke zwischen Anzahl der Artikel der Namen und der Kürzel.
Wenn wir also die Verteilung der Anzahl der geschriebenen Artikel für das Kürzel mit der des vollen Namens vergleichen, ohne diesen Unterschied miteinzubeziehen, enden wir mit einer anderen, weniger aussagekräftigen Earth Mover's Distance.
Nachdem ich die Skalierung durchgeführt habe, sieht die Artikelverteilung für den Autoren von oben wie folgt aus:
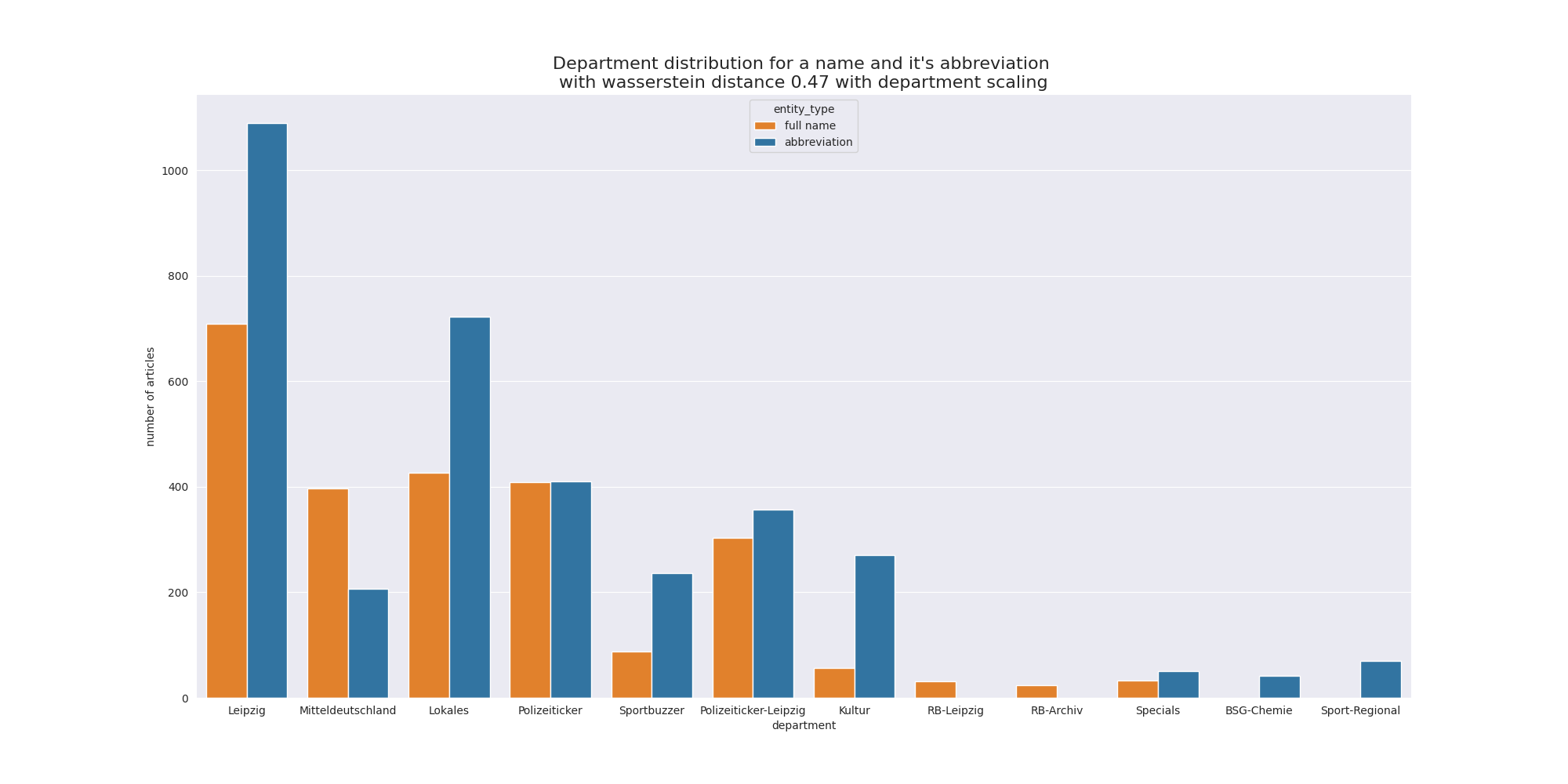
Derselbe Name, dasselbe Kürzel nun aber mit Skalierung.
Wir bemerken, dass zum Beispiel bei dem Ressort Polizeiticker-Leipzig die Balken nun viel näher aneinander sind. Werfen wir nochmal einen Blick auf die unskalierte Grafik und die allgemeine Grafik der Ressorts oben, dann sehen wir, dass das Polizeiticker-Ressort ein allgemeines Verhältnis ca. 17 zu 83 Prozent hat und für den Autor ein sehr ähnliches Verhältnis. Deshalb ist es nach der Skalierung nun fast identisch. Die Distanz liegt nun nur noch bei 0,47.
Validierung
Mit das schwerste an dieser Analyse ist, dass ich kein Validationsset habe. Ich kann also nicht überprüfen, ob die Zuordnung richtig war. Ich versuche meine Analyse anhand von anderen Metriken zu validieren. Weiter oben habe ich schon beschrieben, wie ich das semantische Mapping validiert habe. Nun sind zwei weitere Scores hinzugekommen. Nach dem Berechnen der beiden anderen Scores, Frequenzmatching und Ressortangehörigkeitsmatching prüfte ich erst einmal, wie die drei Punktzahlen miteinander korrelieren. Es stellt sich heraus, dass alle positiv miteinander korrelieren.
Ko-Autorenschaft
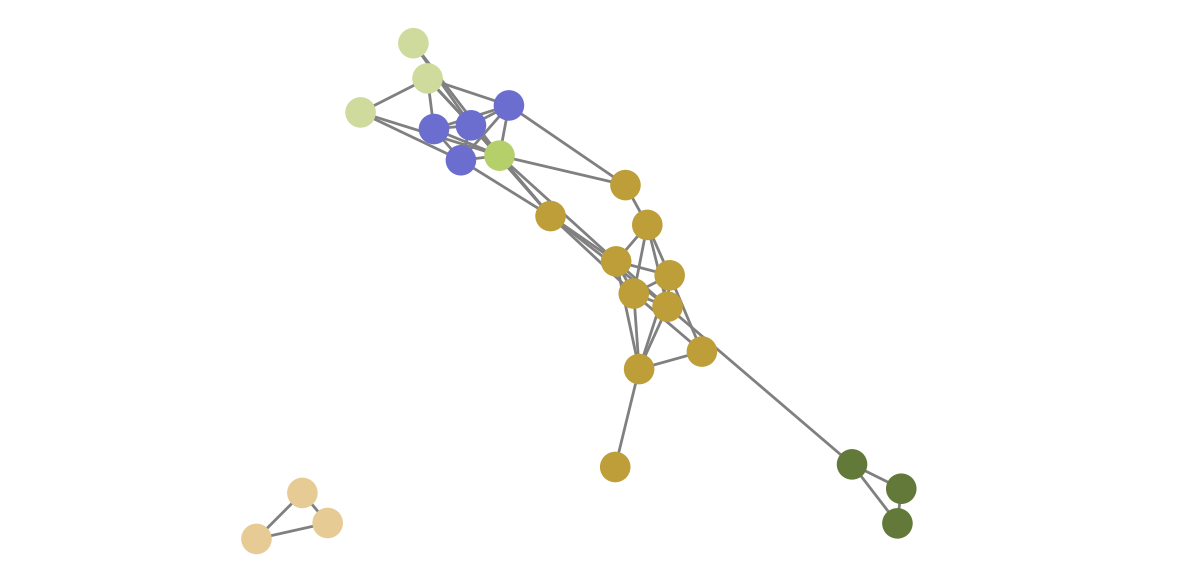
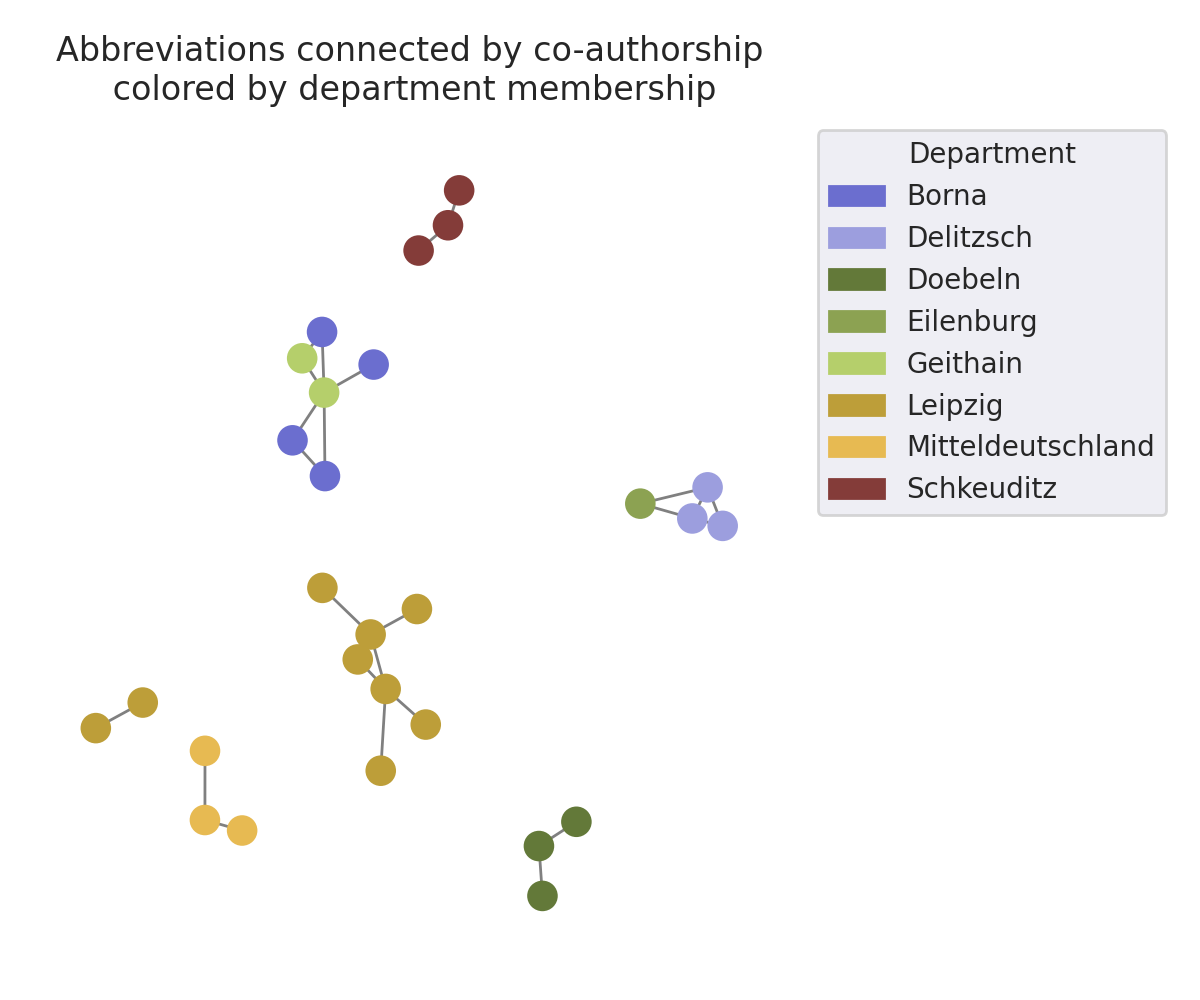
Artikel der LVZ werden auch gerne mal von zwei oder mehr Personen geschrieben. Wir können diese Zusammenarbeit mit einem Graphen sehr gut plotten. Die Kanten markieren dabei die Zusammenarbeit. Im Folgenden sieht man einen solchen Graphen für eine Auswahl an Autor:innen, die ich nach ihrer Hauptressortmitgliedschaft eingefärbt habe.
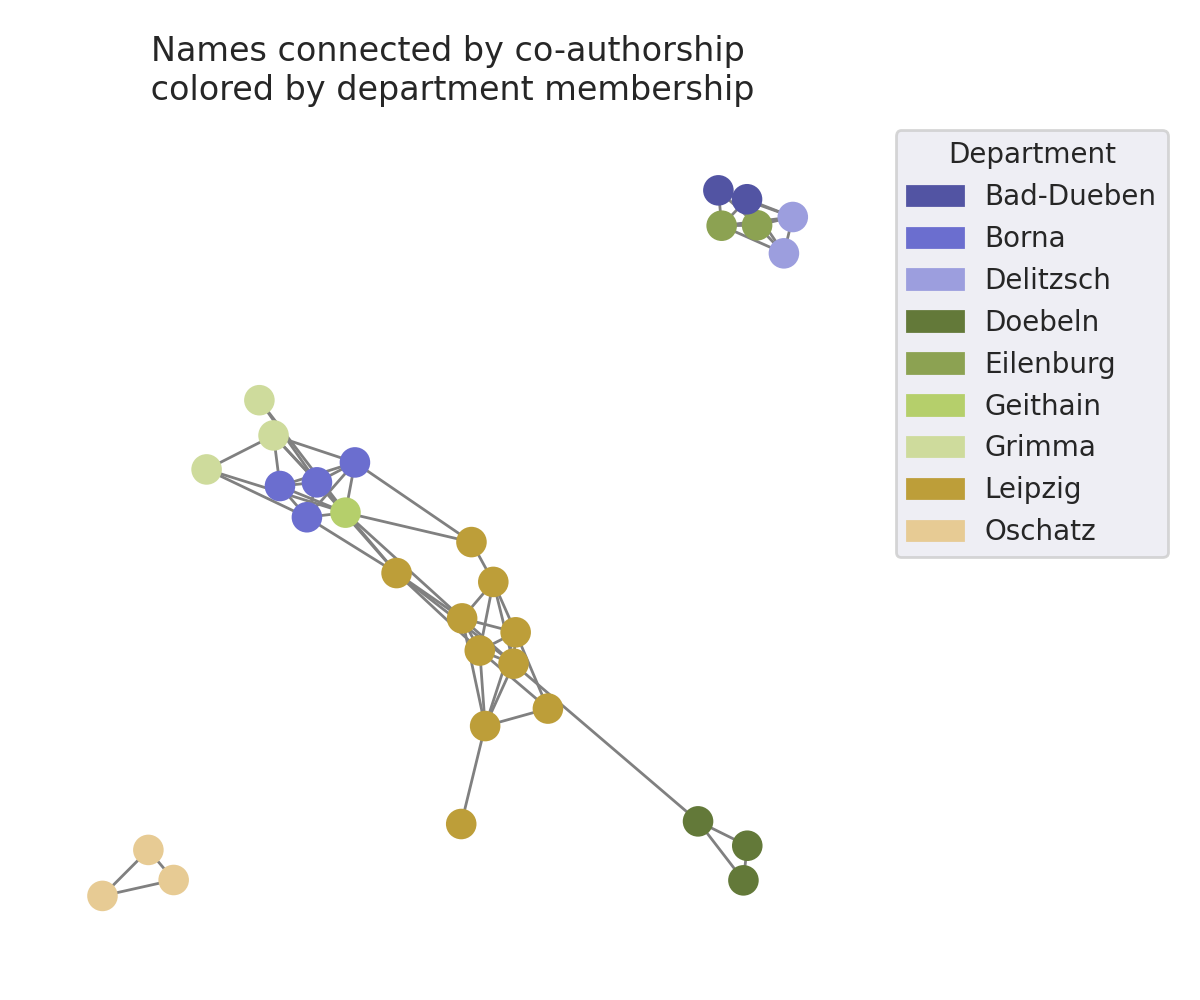
Nun teste ich, ob nach durchgeführtem Matching diese Karte der Zusammenarbeit von den Kürzeln ähnlich zu der, der gematchten Namen aussieht. In unserem fiktiven Beispiel: Nehmen wir an, dass „GH“ auf Gudrun Hagen gemappt wurde und „Wol“ auf Wolfgang Lehmann. Wenn „GH“ und „Wol“ viel zusammenarbeiten, dann sollten das auch Gudrun Hagen und Wolfgang Lehmann tun.
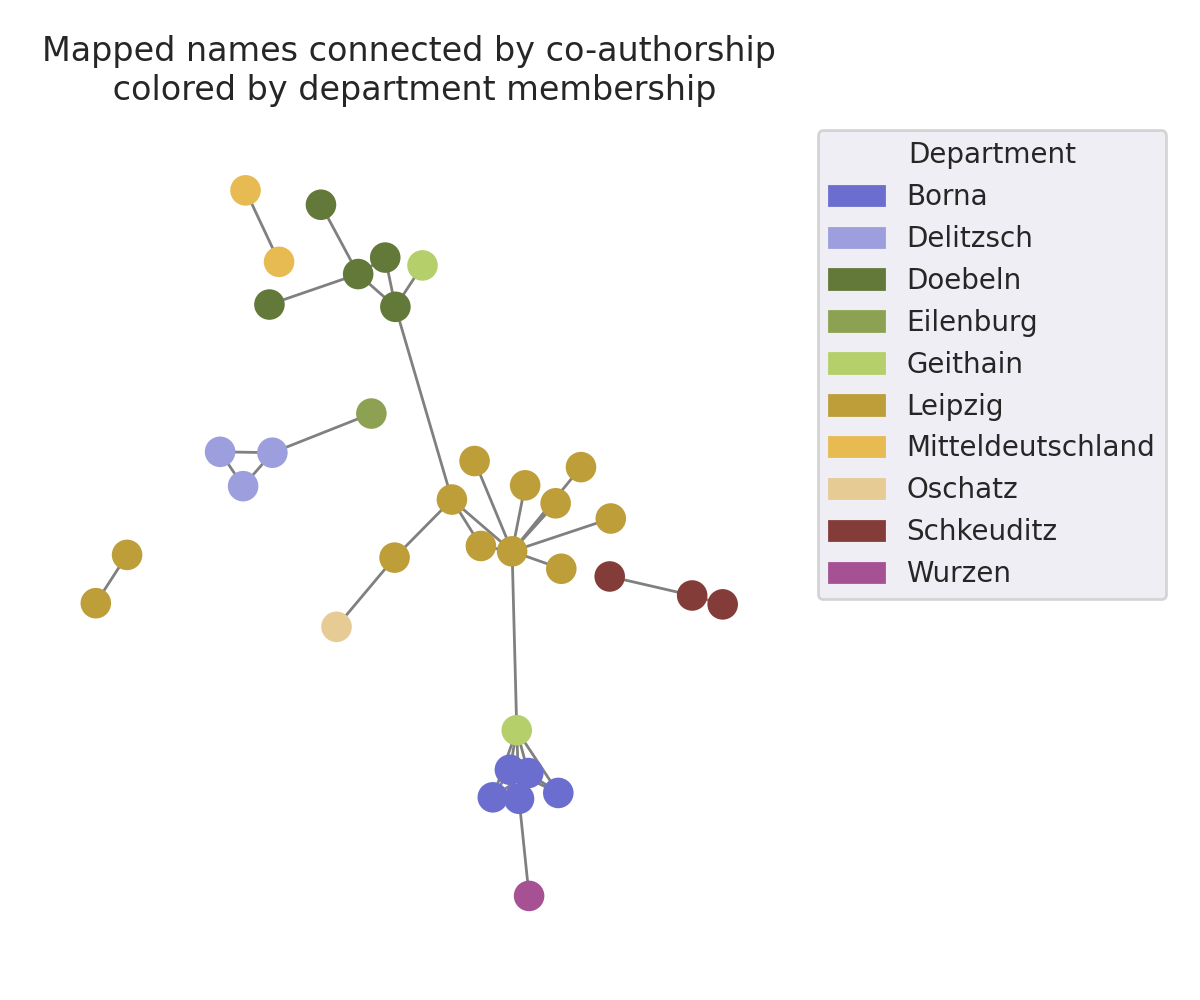
Links sehen wir die Kürzel und ihre Kollaborationen und rechts die der gemappten Namen. Wir sehen tatsächlich eine ähnliche Clusterbildung. Es gibt eins für Leipzig, eins für Mitteldeutschland, Schkeuditz, Borna zusammen mit Geithain und so weiter.
Führen wir die Fäden zusammen
Wir haben nun drei Metriken, um das Mapping durchzuführen. Dazu bauen wir uns einen bipartiten Graphen. Auf der einen Seite die Knotenmenge der Namen auf die der Kürzel. Wir zeichnen die Kanten für die möglichen Mappings ein und versehen sie mit der Summe unserer drei Scores als ihr Gewicht.
Ziel ist es nun, ein Matching mit den minimalen Kosten zu finden. Das Ganze ist als Assignment Problem bekannt und wird zum Beispiel sonst gelöst, wenn Studierende mit gewählten Prioritäten auf Modulplätze verteilt werden. Dabei bleibt eine Menge an Kanten, deren Kardinalität so groß ist, wie die kleinere Menge an Knoten meines bipartiten Graphen. Ich füge der Menge an Kürzeln künstlich noch Dummy Knoten hinzu. Pro Namen gibt es einen Dummy mit einem Gewicht, was einem unsicheren Score gleichkommt. Dadurch erlaube ich dem Algorithmus auch, einem Namen kein Kürzel zuzuordnen. Andersherum tue ich das nicht. Die Annahme ist, dass es für jedes Kürzel einen Namen gibt. Die Dummys entferne ich nach der Berechnung wieder.
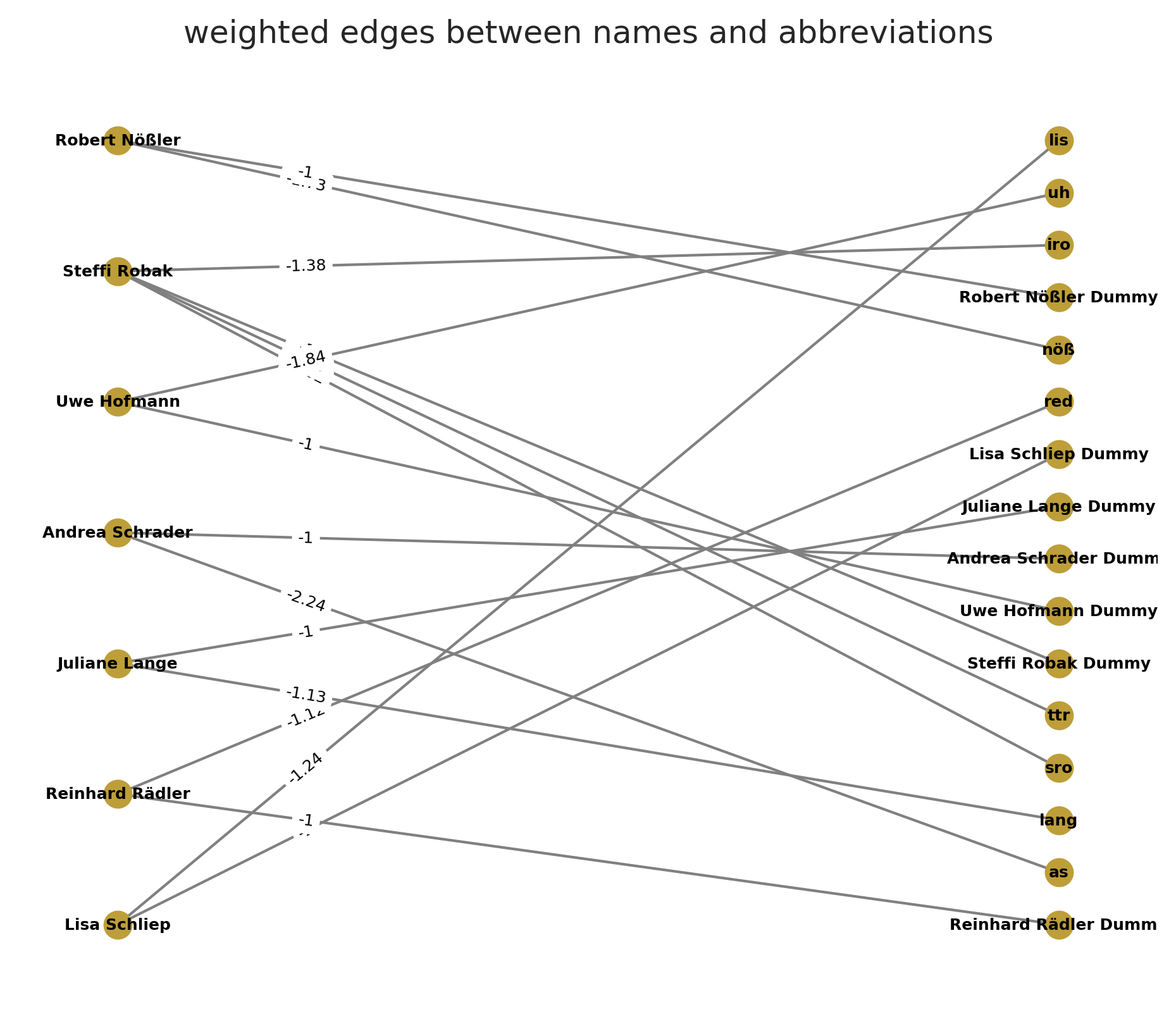
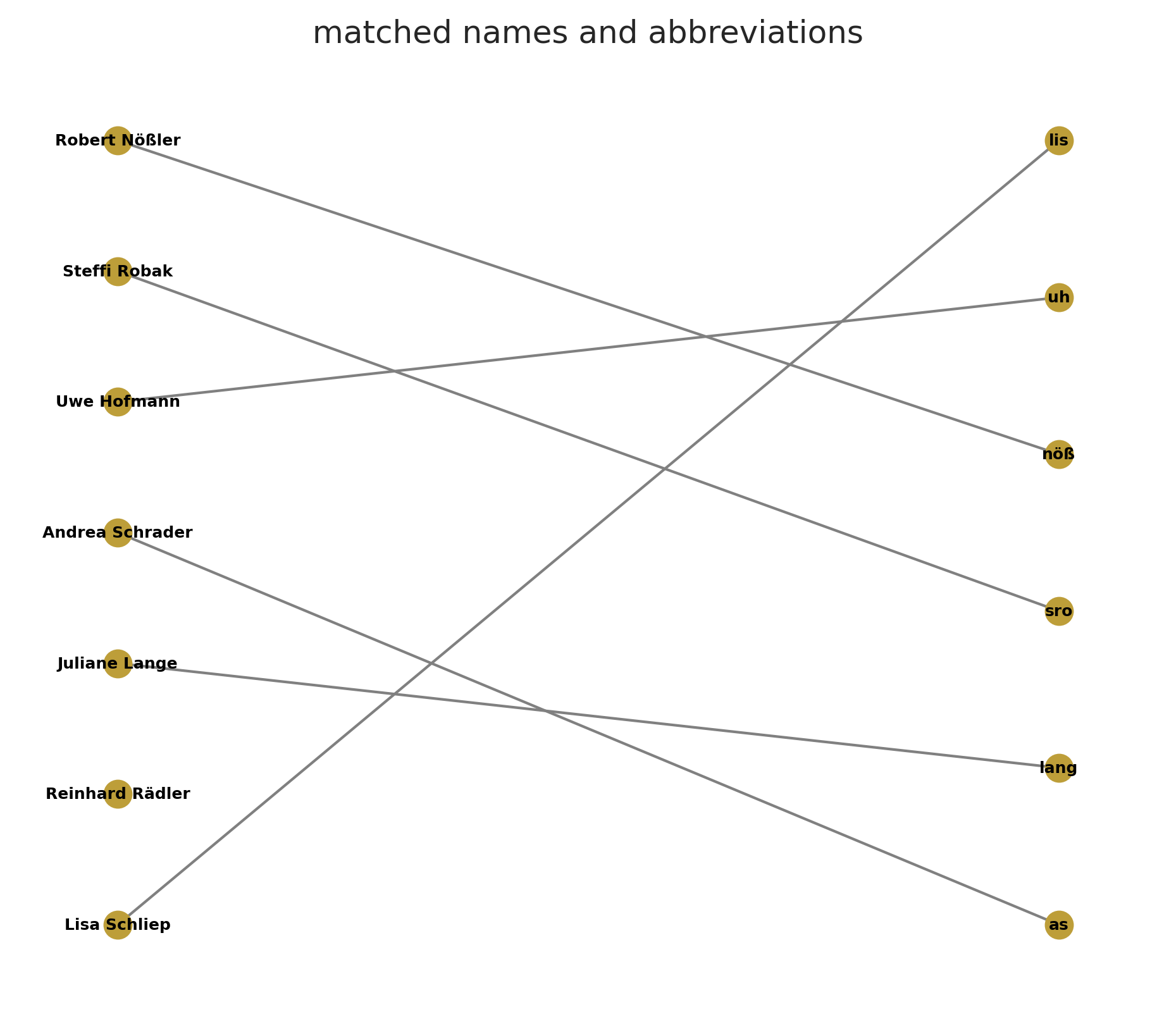
Das Assignment Problem: Die Gewichte sind negativ (Vorzeichen gedreht) damit der Algorithmus sie minimieren kann.
Das Mapping schafft es, von 174 Kürzeln 137 erfolgreich zuzuordnen. Also immerhin fast 80 Prozent. Die Restlichen verbleiben ohne Match. Nicht wundern: Es gibt mehr Kürzel als 174, die wurden aber wegen zu wenigen Artikeln schon im Vorfeld meiner Analyse aussortiert.
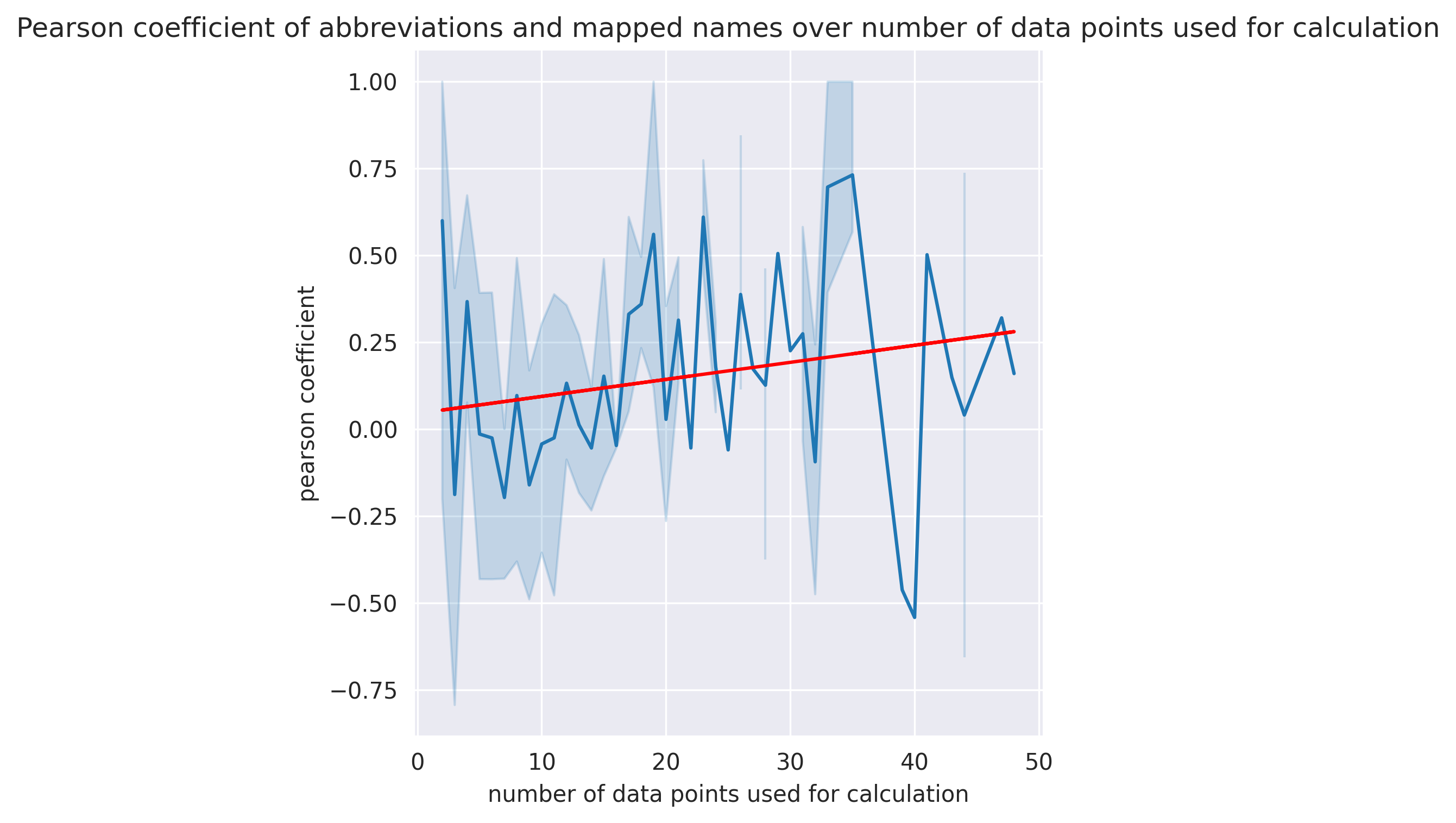
Kalkulieren wir ein letztes Mal die Korrelation zwischen den Artikelverteilungen der Kürzel und ihren gematchten Namen. Herauskommt der Wert 0,12. So scheint es, dass die weiteren Metriken das Mapping verbessert haben, wenn auch nicht übermäßig. Aber wie oben auch schon erörtert, ist weiterhin fraglich, welchen Korrelationsscore ein perfektes Matching überhaupt erreichen könnte.
Niclas Stoffregen, 27.01.2024